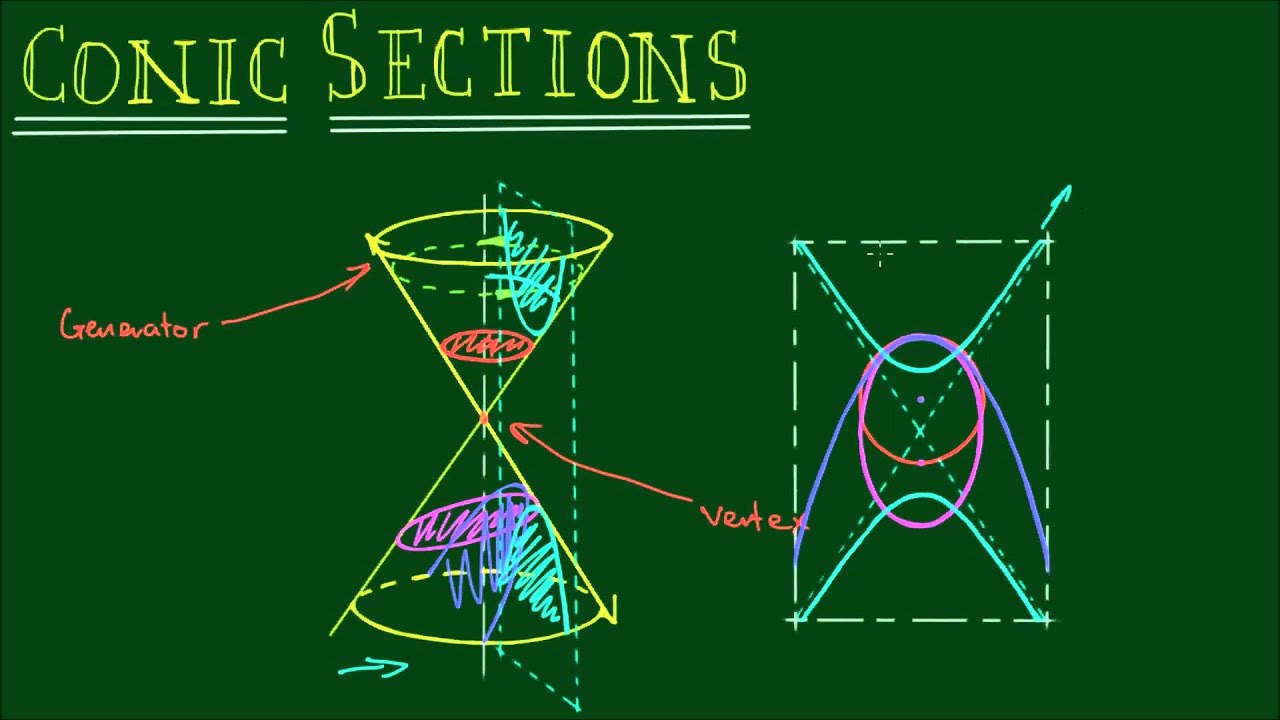
A conic section can be defined as the conic derived from the intersections of a plane with that of a cone. Based on their orientation, the angle between the cone and the plane, they can be classified into parabola, ellipse, hyperbola, a circle (also called a special case of an ellipse).
This page talks about the concept of conic sections and a few JEE Main conic sections previous year solved problems. These solutions are explained in detail for the benefit of the students. Conic sections are explained on the Euclidean plane that involves determining properties. The parameters of the conic include the following. The collection of points that is at a distance from a fixed point and a specific line, that is, a directrix is called the focus. Based on the value of eccentricity, the different types of conic sections are as follows:
- 0 < e < 1 – ellipse
- e = 1 – a parabola
- e > 1 – a hyperbola
- e = 0 – circle
The principal axis is the line that connects the foci of the conic and the midpoint that is the curve’s centre. A chord passing through the focus and parallel to the fixed line that is the directrix is the latus rectum. Semi latus rectum is the half of the latus rectum. The distance covered between the specific directrix and the focus is the focal parameter. The chord between the two vertices is the major axis and the diameter that is the shortest can be called the minor axis. The half lengths of the major and minor axis are the semi-major and semi-minor axes. The table given below explains the different values of conic sections based on their equation and properties.
| Conic Section | Equation | Semi Latus Rectum | Focal Parameter |
| Circle | x2 + y2 = a2 | a | ∞ |
| Ellipse | (x2 / a2) + (y2 / b2) = 1 | b2 / a | b2 / √a2 – b2 |
| Parabola | y2 = 4ax | 2a | 2a |
| Hyperbola | (x2 / a2) – (y2 / b2) = 1 | b2 / a | b2 / √a2 + b2 |
- If b2 − 4ac < 0 – represents ellipse equation
- If a = c and b = 0 – represents circle equation
- If b2 − 4ac = 0 – represents parabola equation
- If b2 − 4ac > 0 – represents hyperbola equation
- If a + c = 0 – represents rectangular hyperbola equation
Solved Problems On Conic Sections
Question 1: The equation 2x2 + 3y2 = 30 represents
1) A circle
2) An ellipse
3) A hyperbola
4) A parabola
Solution: (2) An ellipse
x2 / (30 / 2) + y2 / (30 / 3) = 1
(x2 / 15) + (y2 / 10) = 1
Question 2: The one which does not represent a hyperbola is
1) xy = 1
2) x2 – y2 = 5
3) (x – 1) (y – 3) = 3
4) x2 – y2 = 0
Solution: (4) x2 – y2 = 0
For hyperbola Δ ≠ 0 and h2 > ab.
Here Δ = 0.
Question 3: The locus of the point which moves such that the ratio of its distance from two fixed points in the plane is always a constant k (< 1) is
1) Hyperbola
2) Ellipse
3) Straight line
4) Circle
Solution: (2) Ellipse
In the case of an ellipse, the locus of the point moves such that the ratio of its distance from two fixed points in the plane is always a constant k (< 1). For more information on conic sections and problems of conic sections, please visit BYJU’S website. It consists of problems and solutions for almost all the maths topics for IIT-JEE, GMAT, CET, GATE and other competitive examinatio